This is a quick update on a small problem I worked on. I wanted to write an algorithm for computing a convex hull — just for practice.
A (2D) convex hull is the minimum convex polygon that encapsulates all points in a given set. This took me much longer to figure out than I hoped: it took three stabs for me to come up with the right algorithm (in pseudocode), and it was very frustrating to debug the actual implementation. In retrospect, I probably would’ve made my life much easier if I had followed test-driven development. It doesn’t help that it’s tricky to work with angles in code because they loop back around (i.e. \(2\pi = 0\)). Anyway here’s the implementation I came up with (also included below). I’ve detailed the intuition behind the algorithm below. Be warned: I haven’t sat down and proved that this algorithm actually works, and some of these assumptions/“insights” might be non-trivial. In particular, my algorithm might be dependent on the order of the input points — which should not be the case for the actual minimum polygon.
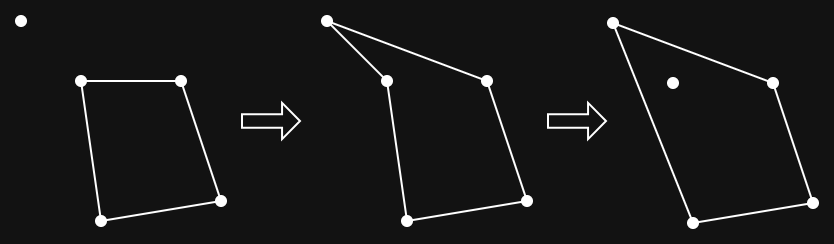
Insight 1: Gradually Expand the Hull
The idea is very simple: instead of computing a hull that encloses all \(n\) points, find one that includes \(i\) points. Then grow this to include the \(i + 1\)th point, then the \(i + 2\)th point, and so on. Note that this is meaningless/trivial for one and two points. Also for three points, the triangle formed by the three points is guaranteed to be the convex hull since all triangles are convex, and trying to reduce the area will always introduce concavity. Thus we always start with \(i = 3\) points by just taking the first three points.
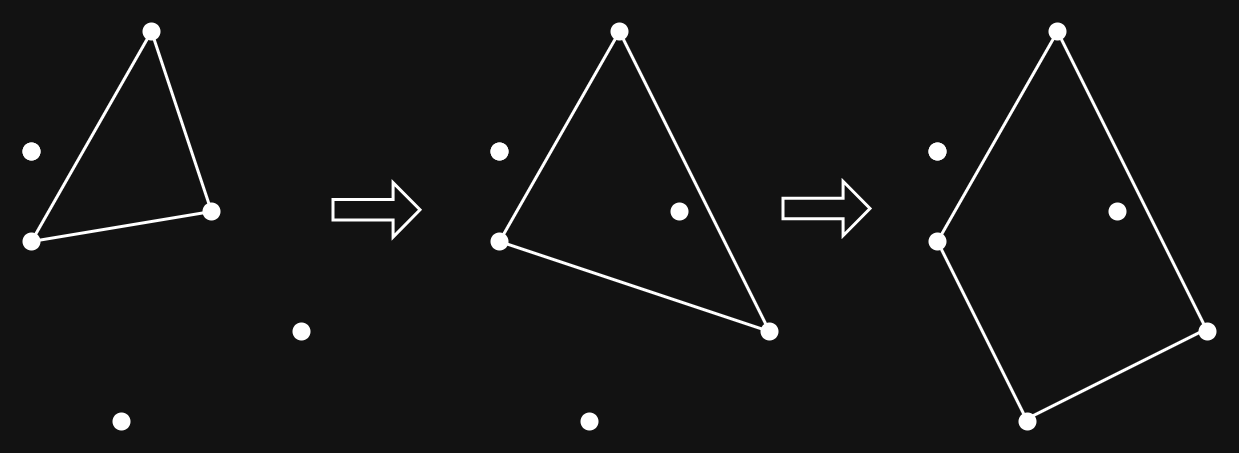
Insight 2: If a Point is within the Hull, Don’t Change Anything
This is pretty straightforward: if a point is already included, then we don’t need to expand or contract the hull. Additionally, we can know that this \(i+1\)th point will continue to be in the hull as long as the other \(i\) points are in hull. This is because it is a convex combination of the existing points. Thus it can be ignored by the rest of the algorithm, and we just need to ensure that all of the first \(i\) points continue to be enclosed.
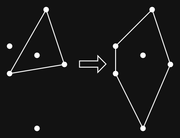
Insight 3: Signed Distances Tell You Where to Insert the New Point
This is related to Insight 2: if the new point is on the right side (i.e. inside vs outside) of an edge, then we don’t need to worry about an edge. If however, it’s on the wrong side, then we’ll have to modify that edge. The edges that need changing will be adjacent, and there should only be 1 or 2 of them in most cases. A simple way to choose an edge is by taking the signed distance between each edge and the new point and then choosing the edge with the minimum signed distance. N.B. I’m using the convention of positive signed distance for points on the inside of the edge.
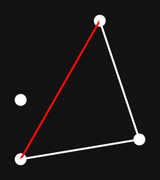
Insight 4: Remove Points to Resolve Concavity
Often, when you apply insight 3, you get the convex hull you’re looking for i.e. all previous points are still included, the new point is also included, and the resulting polygon is convex. There are some cases where the resulting shape is now concave. You can detect this by checking if the newly formed angles are reflex angles (greater than 180°). You can then safely remove the invalid vertex since the reflex angle guarantees that the removed point is now in the interior of the polygon. Finally, you can repeat this process until all reflex angles are removed.